Table Of Content

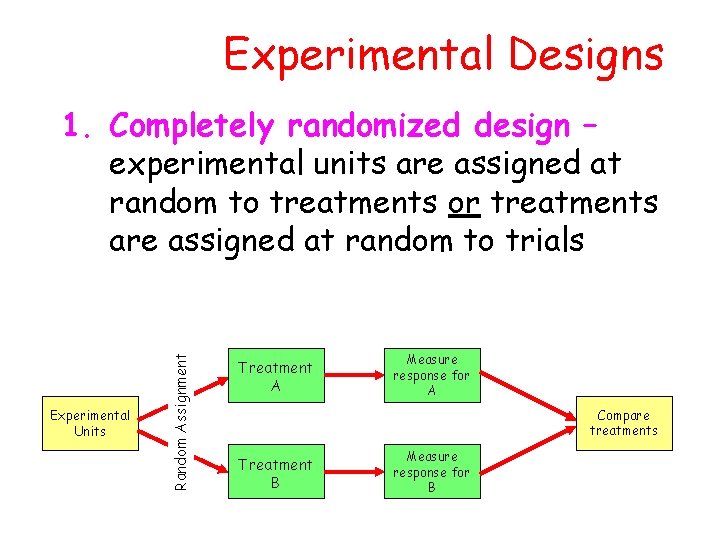
Ideally, experiments should be run by using completely randomized experimental units. However, often, there is not enough experimental units from one homogenous sample. For example, if there are not enough raw materials to produce all the experimental units for all replications, blocking is utilized to control the nuisance effects of the experimental units coming from, possibly non homogenous batches. Different batches do not necessarily mean non-homogeneity all the time. However, keeping track of the batch numbers as blocks (the statistical term) would provide an opportunity, if in case there is non-homogeneity from batch to batch.
Batch
Here as with all crossover designs we have to worry about carryover effects. We let the row be the machines, the column be the operator, (just as before) and the Greek letter the day, (you could also think of this as the order in which it was produced). Therefore the Greek letter could serve the multiple purposes as the day effect or the order effect. As the treatments were assigned you should have noticed that the treatments have become confounded with the days.
Development of liposomes using formulation by design: Basics to recent advances - ScienceDirect.com
Development of liposomes using formulation by design: Basics to recent advances.
Posted: Fri, 11 Oct 2019 12:43:04 GMT [source]
4 Randomised complete block designs
When we have missing data, it affects the average of the remaining treatments in a row, i.e., when complete data does not exist for each row - this affects the means. When we have complete data the block effect and the column effects both drop out of the analysis since they are orthogonal. With missing data or IBDs that are not orthogonal, even BIBD where orthogonality does not exist, the analysis requires us to use GLM which codes the data like we did previously. For an odd number of treatments, e.g. 3, 5, 7, etc., it requires two orthogonal Latin squares in order to achieve this level of balance. For even number of treatments, 4, 6, etc., you can accomplish this with a single square. This form of balance is denoted balanced for carryover (or residual) effects.
4.2 Nesting Blocks
Nesting them enables estimation of their respective variance components, while crossing leads to row-column designs that control for two sources of variation simultaneously. Nesting blocking factors allows us to replicate already blocked designs, to combine several properties for grouping, and to disentangle the variance components of different levels of grouping. We consider only designs with two nested blocking factors, but our discussion directly extends to longer chains of nested factors. In contrast to a two-way ANOVA with factorial treatment structure, we cannot simplify the analysis to a one-way ANOVA with a single treatment factor with \(b\cdot k\) levels. This is because the blocking factor is random, and the resulting one-way factor would also be a random factor. The omnibus \(F\)-test for this factor is difficult to interpret, and a contrast analysis would be a futile exercise, since we would compare randomly sampled factor levels among each other.
Want to Pass Your Six Sigma Exam the First Time through?
Here is an actual data example for a design balanced for carryover effects. In this example the subjects are cows and the treatments are the diets provided for the cows. Using the two Latin squares we have three diets A, B, and C that are given to 6 different cows during three different time periods of six weeks each, after which the weight of the milk production was measured. We have not randomized these, although you would want to do that, and we do show the third square different from the rest.
ANOVA: Yield versus Batch, Pressure
And let's say you're purchasing packaged bread dough from some food company rather than mixing it yourself. Here is a concise answer.A lot of details and examples might be found in most documents treating the design of experiments; especially in agronomy. For this experiment, treatments 1 and 3, 1 and 4, 2 and 3, and 2 and 4 are significantly different at an experiment-wise type I error rate of 5%. You can obtain the 'least squares means' from the estimated parameters from the least squares fit of the model.
Blocking used for nuisance factors that can be controlled
For an incomplete block design, the incidence matrix would be 0's and 1's simply indicating whether or not that treatment occurs in that block. We can test for row and column effects, but our focus of interest in a Latin square design is on the treatments. Just as in RCBD, the row and column factors are included to reduce the error variation but are not typically of interest. And, depending on how we've conducted the experiment they often haven't been randomized in a way that allows us to make any reliable inference from those tests. The Latin Square Design gets its name from the fact that we can write it as a square with Latin letters to correspond to the treatments.
3 - The Latin Square Design
We want a design with 3 blocking factors; machine, operator, and day of the week. Situations where you should use a Latin Square are where you have a single treatment factor and you have two blocking or nuisance factors to consider, which can have the same number of levels as the treatment factor. At a high level, blocking is used when you are designing a randomized experiment to determine how one or more treatments affect a given outcome. More specifically, blocking is used when you have one or more key variables that you need to ensure are similarly distributed within your different treatment groups.
4.3 Crossing Blocks: Latin Squares
Most of thevariables inspected so far have divided the samples into nonoverlappingcategories, this will however not always be the case. Often, variablesare continuous or categories are overlapping, such as age or diseasestate, respectively. Categories that span a large number of valuescan lead to relatively large differences between subjects within acategory, while the differences between subjects at the edges of neighboringcategories will be small. On the other hand, in a large enough studythe randomization should mitigate this problem. Additionally, a substantialnumber of subjects per category is a requirement to still be ableto randomize subjects. If each subject ends up being its own category,randomization will no longer be possible.
Blocking NS3–NS4B interaction inhibits dengue virus in non-human primates - Nature.com
Blocking NS3–NS4B interaction inhibits dengue virus in non-human primates.
Posted: Wed, 15 Mar 2023 07:00:00 GMT [source]
This design allows us to fully remove thebetween-block variability, e.g., variability between different locations, fromthe response because it can be explained by the block factor. If we carefully select the blocking factors, we can assume these interactions to be negligible and arrive at the much simpler experiment design in Figure 7.12D. Our experiment again uses 24 mice, with four litters per laboratory, and each litter is a block with one replicate per drug.
Finally, we might use the same row and column factor levels in each replicate. Essentially, this fully crosses the latin square with a new blocking factor and leads to the model specification y ~ drug + Error(rep+device+tech) or y ~ drug + (1|rep) + (1|device) + (1|tech) for Figure 7.15F. First, we might consider replicating columns while keeping the rows, using \(rk\) column factor levels instead of \(k\).
The complexity of the samples,the proteome, and the analytical techniques employed make proteomicsexperiments particularly challenging. Especially in larger studies,the labor intensive sample preparation often means that the experimenthas to be split into multiple batches. It is therefore important todesign the experiment in such a way that variables and batches arenot confounding. When the size of the batches is insufficient toachieve this, it is essential to make sure that the utilized experimentaldesign can give answers to the scientific questions asked.
The most common blocking design is the randomized complete block design, where each treatment occurs once per block. Its analysis requires the assumption of no block-by-treatment interaction, which the experimenter can ensure by suitable choice of the blocking factor. The efficiency of blocking is evaluated by appropriate effect sizes, such as the proportion of variation attributed to the blocking. It typically deteriorates if the block size becomes too large, since experimental units then become more heterogeneous.
With the increasing maturity of the text-to-image and image-to-image generative models, AI-generated images (AGIs) have shown great application potential in advertisement, entertainment, education, social media, etc. Although remarkable advancements have been achieved in generative models, very few efforts have been paid to design relevant quality assessment models. In this paper, we propose a novel blind image quality assessment (IQA) network, named AMFF-Net, for AGIs. AMFF-Net evaluates AGI quality from three dimensions, i.e., "visual quality", "authenticity", and "consistency". After that, an Adaptive Feature Fusion (AFF) block is used to adaptively fuse the multi-scale features with learnable weights.
To conduct this experiment as a RCBD, we need to assign all 4 pressures at random to each of the 6 batches of resin. Each batch of resin is called a “block”, since a batch is a more homogenous set of experimental units on which to test the extrusion pressures. Below is a table which provides percentages of those products that met the specifications. In our previous diet pills example, a blocking factor could be the sex of a patient.

No comments:
Post a Comment